什么是索引?什么是索引?索引原理
什么是索引(什么是索引?索引原理)索引是单独的,物理的对数据库表中一列或多列的值进行排序的一种存储结构,让程序能够快速找到所需内容。
索引是一种数据结构(平衡树非二叉),即B树,B+树,通过不断的缩小想要获得数据的范围来筛选出最终想要的结果,同时把随机的事件变成顺序的事件。
B树:
1.定义任意非叶子结点最多只有M个儿子;且M>2;
2.根结点的儿子数为[2, M];
3.除根结点以外的非叶子结点的儿子数为[M/2, M];
4.每个结点存放至少M/2-1(取上整)和至多M-1个关键字;(至少2个关键字)
5.非叶子结点的关键字个数=指向儿子的指针个数-1;
6.非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
7.非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的
子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树;
8.所有叶子结点位于同一层;
B-树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果
命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为
空,或已经是叶子结点;
B-树的特性:
1.关键字 *** 分布在整颗树中;
2.任何一个关键字出现且只出现在一个结点中;
3.搜索有可能在非叶子结点结束;
4.其搜索性能等价于在关键字全集内做一次二分查找;
5.自动层次控制;
由于限制了除根结点以外的非叶子结点,至少含有M/2个儿子,确保了结点的至少
利用率,其更底搜索性能为:
其中,M为设定的非叶子结点最多子树个数,N为关键字总数;
所以B-树的性能总是等价于二分查找(与M值无关),也就没有B树平衡的问题;
由于M/2的限制,在插入结点时,如果结点已满,需要将结点分裂为两个各占
M/2的结点;删除结点时,需将两个不足M/2的兄弟结点合并;
B+树是B-树的变体,也是一种多路搜索树:
1.其定义基本与B-树同,除了:
2.非叶子结点的子树指针与关键字个数相同;
3.非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树
(B-树是开区间);
5.为所有叶子结点增加一个链指针;
6.所有关键字都在叶子结点出现;
B+的特性:
1.所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好
是有序的;
2.不可能在非叶子结点命中;
3.非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储
(关键字)数据的数据层;
4.更适合文件索引系统;

相关文章
搜索引擎原理:你根本不懂的优化缘由
今天和朋友讨论到一个网站站内优化的时候,发现了一个很普偏的错误现象,就是大家都不明白搜索引擎原理,而麻木的看人家怎么优化,我们就怎么优化,所以一直以来优化不出啥名堂来。 为何要使用H标签? 朋...
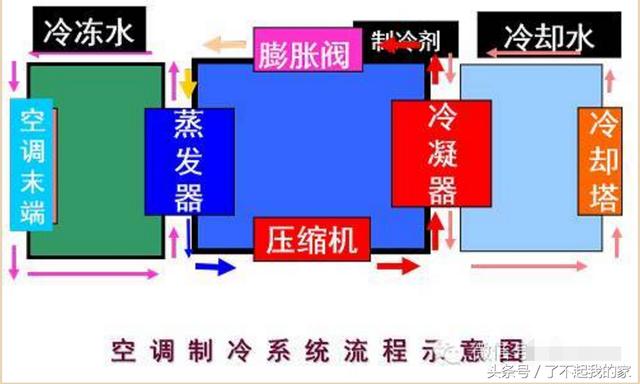
家用中央空调结构原理图解
什么是中央空调系统 1.空调:即空气调节器,是一种用于给空间区域进行空气处理的机组。主要是对封闭空间或区域内空气的温度、湿度、洁净度和流速等参数进行调节,以满足人体舒适或工艺流程的要求。 2.中央...
电鳗为什么会放电?电鳗放电的原理
电鳗在水里放电,为何自己不会被电,它们到底怕不怕电? 在我们所身处的这个自然界中,有着各种形形色色的生物存在,人类也只是其中的一员。而在自然界中有着许多动物们,他们的一些能力让即使有发达文明的人类也...
Session什么意思?一文带你超详细了解Session的原理及应用
session 简介 session 是我们 jsp 九大隐含对象的一个对象。 session 称作域对象,他的作用是保存一些信息,而 session 这个域对象是一次会话期间使用同一个对象。所以...
核酸检测是什么意思?新冠病毒核酸检测原理是什么?
核酸检测是什么意思(新冠病毒核酸检测原理是什么?)新冠病毒突如其来,打的每一个中国人都是措手不及。现在依旧处于新冠病毒防范的关键期,我们也越来越多的看到核酸检测依旧是确诊和出院的诊断标准,也是被专家组...
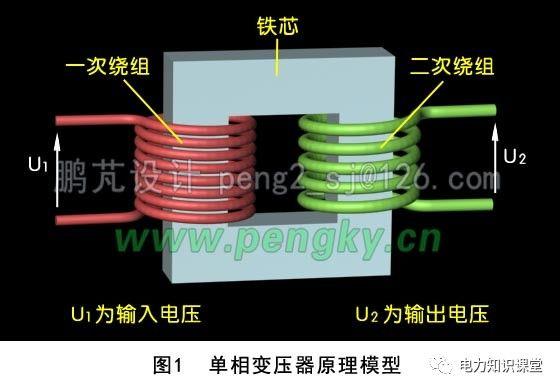
变压器原理(附详细图解)一看就懂
图1是单相变压器的原理模型,由铁心与套在铁心上的两个绕组组成,铁心由导磁性能好、磁滞损耗小的材料制成。与电源相连的线圈为一次绕组,与负载相连的线圈为二次绕组。 U1为输入一次绕组的电压,N1为一次绕组...




 免责声明:本站所发布的任何网站,全部来源于互联网,版权争议与本站无关。仅供技术交流,如有侵权或不合适,请联系本人进行删除。不允许做任何非法用途!
免责声明:本站所发布的任何网站,全部来源于互联网,版权争议与本站无关。仅供技术交流,如有侵权或不合适,请联系本人进行删除。不允许做任何非法用途!