什么是微分?微积分的本质到底是什么?
微积分的本质可以从物理上求速度和位移来说明!
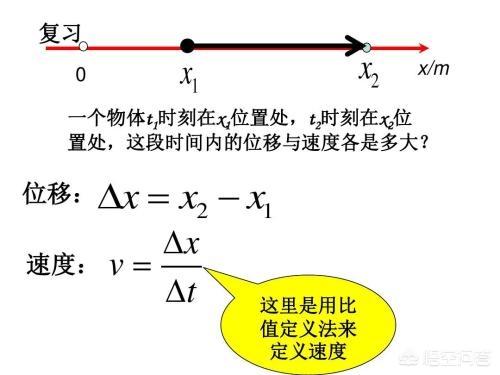
首先,说微分。没有这个概念以前,高中物理最多敢讲授匀变速运动。唯一涉及到变加速运动还是在功里面,通过汽车加速过程中,通过不断增加档位,减小牵引力,提高速度,最终达到匀速。大学里面解决这一问题就简单了,我们可以假设如上图的,如果
t2—t1无限趋紧于0,则这时:
v=ds/dt,即由上图的平均速度变成了瞬时速度,这就是求位移对时间的导数。可见,小伙伴再也不是只能计算匀速、匀变速运动了,任何运动都可以用导数来计算。总结来说,就是微分就是如果我们将复杂的变加速运动速度,分割成很多的极短时间的匀速运动,就可以计算出物体各个时刻的速度了。
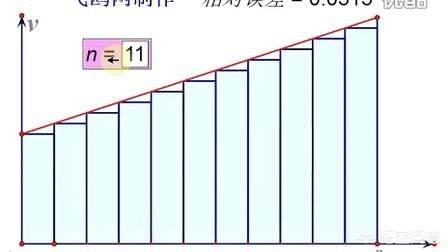
其次说积分。没有积分以前,我们也只能通过运动学公式计算匀速或者匀变速物体的位移。而有了积分我们面对变速运动也可以通过计算每一段不同速度的位移再加起来就可以了。如上图所示,只要我们把每一段的时间的位移进行叠加,就可以近似得到总的位移。分的时间段越小,最后叠加以后就越接近真实的位移。因此,变速运动的位移也就通过积分得到解决了!
相关文章
微积分公式(微积分公式运算法则)
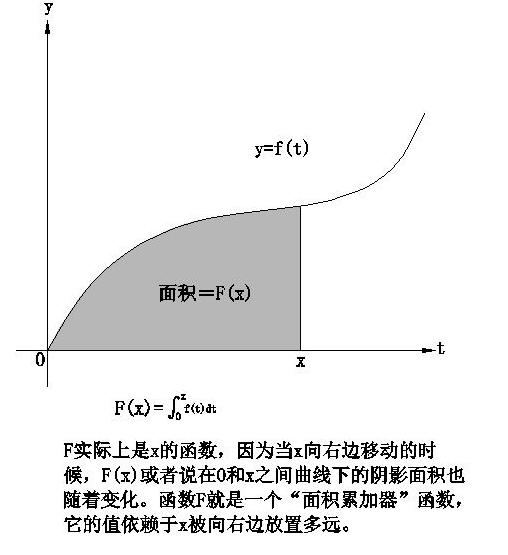
微积分公式(微积分公式运算法则)对于曲线下的阴影面积,可以表示为一个函数F(x),现在的问题是,如何构建函数表达式? 阴影面积可以使用黎曼积分的一元方程,通过分割、近似、求和、取极限去计算...
 免责声明:本站所发布的任何网站,全部来源于互联网,版权争议与本站无关。仅供技术交流,如有侵权或不合适,请联系本人进行删除。不允许做任何非法用途!
免责声明:本站所发布的任何网站,全部来源于互联网,版权争议与本站无关。仅供技术交流,如有侵权或不合适,请联系本人进行删除。不允许做任何非法用途!