主成分分析法步骤与优缺点(主成分分析法教你降维打击)

本文的目的是为主成分分析(PCA)提供一个完整且简单的解释,特别是其运作方式,以增进大家对该分析法的理解并加以利用,而不必具有强大的数学背景。
PCA实际上是网上广泛提及的一种 *** ,很多文章都有涉及。但是,只有极少数文章能直接切入主题,并在不过多钻研技术细节的前提下解释PCA的工作原理以及“为什么”。这就是这篇文章的目的:以更简单的方式解释主成分分析法。
在开始解释之前,本文提供了PCA在每一步骤的运作原理的逻辑解释,简化了其背后的数学概念,如标准化,协方差,特征向量和特征值,而暂未关注如何运算的问题。

什么是PCA?
PCA是一种常用于减少大数据集维数的降维 *** ,把大变量集转换为仍包含大变量集中大部分信息的较小变量集。
减少数据集的变量数量,自然是以牺牲精度为代价的,降维的好处是以略低的精度换取简便。因为较小的数据集更易于探索和可视化,并且使机器学习算法更容易和更快地分析数据,而不需处理无关变量。
总而言之,PCA的概念很简单——减少数据集的变量数量,同时保留尽可能多的信息。

逐步解释
第1步:标准化
这一步的目的是把输入数据集变量的范围标准化,以使它们中的每一个均可大致成比例地分析。
更具体地说,在使用PCA之前必须标准化数据的原因是PCA对初始变量的方差非常敏感。也就是说,如果初始变量的范围之间存在较大差异,那么范围较大的变量将占据范围较小的变量(例如,范围介于0和100之间的变量将占据0到1之间的变量),这将导致主成分的偏差。因此,将数据转换为可比较的比例可避免此问题。
在数学上,这一步可以通过减去平均值,再除以每个变量值的标准偏差来完成。

只要标准化完成后,所有变量都将转换为相同的范围[0,1]。
第2步:协方差矩阵计算
这一步的目的是:了解输入数据集的变量是如何相对于平均值变化的。或者换句话说,是为了查看它们之间是否存在任何关系。因为有时候,变量间高度相关是因为它们包含大量的信息。因此,为了识别这些相关性,我们进行协方差矩阵计算。
协方差矩阵是p×p对称矩阵(其中p是维数),其所有可能的初始变量与相关联的协方差作为条目。例如,对于具有3个变量x,y和z的三维数据集,协方差矩阵是以下的3×3矩阵:

由于变量与其自身的协方差是其方差(Cov(a,a)= Var(a)),因此在主对角线(左上角到右下角)中,实际上有每个起始变量的方差。并且由于协方差是可交换的(Cov(a,b)= Cov(b,a)),协方差矩阵的条目相对于主对角线是对称的,这意味着上三角形部分和下三角形部分是相等的。
作为矩阵条目的协方差告诉我们变量之间的相关性是什么呢?
协方差的重要标志如下:
· 如果为正,则两个变量同时增加或减少(相关)
· 如果为负,则一个减少,另一个增加(不相关)
好了,现在我们知道协方差矩阵只不过是一个表,汇总了所有可能配对的变量间相关性。让我们继续下一步。
第3步:计算协方差矩阵的特征向量和特征值,用以识别主成分
特征向量和特征值都是线性代数概念,需要从协方差矩阵计算得出,以便确定数据的主成分。开始解释这些概念之前,让我们首先理解主成分的含义。
主成分是由初始变量的线性组合或混合构成的新变量。该组合中新变量(如主成分)之间彼此不相关,且大部分初始变量都被压缩进首个成分中。所以,10维数据会显示10个主成分,但是PCA试图在之一个成分中得到尽可能多的信息,然后在第二个成分中得到尽可能多的剩余信息,以此类推。
相关文章
V脸提拉术效果怎么样(脸部提拉手术步骤)
因为松垮下垂的脸最显老!不像斑点、细纹、暗黄、痘痘,还可以用粉底遮一遮,脸一旦垮下来,怎么藏都藏不住! 据某皮肤研究中心调研发现,脸垮往往伴随着皱纹、长色斑、肤色暗黄、脸变宽等面部问题。 脸垮...
微商代理怎么做,做微商的步骤有哪些!
一、新手做微商注意事项: 1、选择一个品牌,花一段时间去了解这个品牌,了解这个这个公司、了解你所要选择的产品!因为只有自己了解了才可以更好的和顾客沟通和介绍!选择一个有控价、效果好、口碑好长线的...
宠物狗训练教程步骤(宠物狗狗如何正确训练)
常见的九大狗狗训练技巧大全: 1、定点大小便训练 训练时间:饭后,喝水后 训练场地: 1)室内定点: ①在饭后或喝水后,把狗狗抱到指定的地方,直到狗狗解决后再抱出来 ②狗狗在其他地方尿...
tplink无线路由器怎么设置密码(tplink无线路由器
TP-link无线路由器是大家常用的路由器,信号稳定,功能强大,用的人很多。所以给大家分享下TP-link无线路由器设置上网的方法,是有必要的。 TP-link无线路由器设置前的网线连接方法: 首...
开淘宝店要多少钱?开淘宝店的流程以步骤
1. 保证金(必须): 普通类目目前还是1000元。部分类目将于2016年10月9日起上调:家具类目的保证金,从1千元上调至5千元、珠宝首饰类目从1千元上调至5千元、平板电脑/MID类目保证金从1千...
支付宝怎么实名认证(支付宝实名认证步骤详解
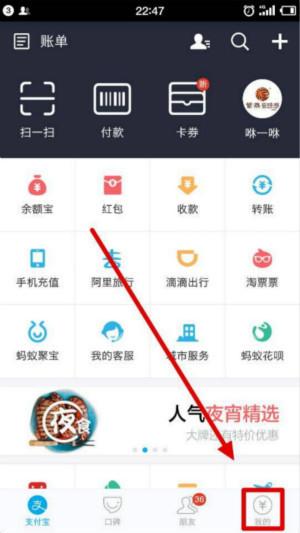
支付宝怎么实名认证(支付宝实名认证步骤详解)1、打开手机支付宝账户,出现以下页面。点击该页面中红色小圈表明的位置“我的”。 2、点击“我的”后,出现以下页面,点击如红框标注的区域 3、接下...





 免责声明:本站所发布的任何网站,全部来源于互联网,版权争议与本站无关。仅供技术交流,如有侵权或不合适,请联系本人进行删除。不允许做任何非法用途!
免责声明:本站所发布的任何网站,全部来源于互联网,版权争议与本站无关。仅供技术交流,如有侵权或不合适,请联系本人进行删除。不允许做任何非法用途!