什么是反函数,举例说明!
一、复合函数
定义:设函数 z = f ( y ) 定义在数集 B ,函数 y = ψ ( x ) 定义在数集 A ,G 是 A 中使 y = ψ ( x ) ∈ B 的 x 的非空子集 (如图1),即
G = { x ∣ x ∈ A, ψ ( x ) ∈ B } ≠ ∅ 。
对任意的 x ∈ G , 按照对应关系 ψ , 对应唯一一个 y ∈ B ,再按照对应关系 f , 对应唯一一个 z(如图1) ,即 对任意的 x ∈ G 都对应唯一一个 z 。于是在 G 上定义了一个函数 , 表为 f • ψ ,称为函数 y = ψ ( x ) 与 z = f ( y ) 的 复合函数 , 即
( f • ψ) (x) = f [ ψ ( x ) ] , x ∈ G , y 称为中间变数(如图2) 。
注:经常将函数 y = ψ ( x ) 与 z = f ( y ) 的复合函数表为 z = f [ ψ ( x ) ] , x ∈ G 。

图(1)

图(2)
例题1、

例题1图
例题2、(三个函数生成的复合函数 )设 u = √z , z = ln y , y = 2x + 3 , 则 u = √[ ln ( 2x + 3 )] , x ∈ [ -1 , + ∞ ] 。
二、反函数
定义:设函数 y = f ( x ) 在数集 A 有定义。
若 对任意的 x1 , x2 ∈ A ,有 x1 ≠ x2 推出 f ( x 1) ≠ f ( x 2) (或 f ( x 1) = f ( x 2) 推出 x1 = x2 ),则称函数 y = f ( x ) 在数集 A 一一对应 。
定义:设函数 y = f ( x ) 在数集 A 一一对应 ,即对任意的 y ∈ f ( A) 只有唯一一个 x ∈ A ,使 f ( x ) = y ,这是一个由 F ( A ) 到 A 的新的对应关系,称为函数 y = f ( x ) 的反函数 , 表示为

反函数图
定理1、若函数 y = f ( x ) 在数集 A 严格增加 (严格减少),则函数 y = f ( x ) 存在反函数,且反函数 x = f^(-1)( y ) 也严格增加(严格减少)。
反函数的性质:
1、单调函数必有反函数。有反函数的函数不一定是单调函数,例如反比例函数 y = K/x ( K ≠ 0 ) ;
2、奇函数不一定有反函数,例如 y = sin x , y = x - 1/x ;当奇函数存在反函数时,反函数一定是奇函数。
例如反比例函数 y = K/x ( K ≠ 0 ) 的反函数还是 y = K/x ( K ≠ 0 ) 。
3、偶函数不一定没有反函数,例如 y = 1 , x ∈ { 0 } 。
反函数与原函数的关系:
1、反函数的定义域是原函数的值域,反函数的值域是原函数的定义域;
2、互为反函数的两个函数的图像关于直线 y = x 对称 ;
3、原函数若是奇函数,则其反函数为奇函数;
4、若函数是单调函数,则一定有反函数,且反函数的单调性与原函数的一致;
5、原函数与反函数的图像若有交点,则交点一定在直线 y = x 上或关于直线 y = x 对称出现 。
原函数 y = f ( x ) 与 反函数 y = f^(-1)( x ) 的图像关于直线 y = x 对称
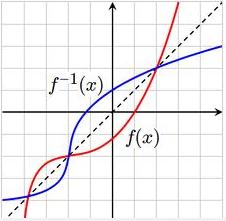
对称图(1)
幂函数中原函数与反函数的图像关于直线 y = x 对称

(2)
指数函数和对数函数互为反函数,图像关于直线 y = x 对称

指数函数与对数函数图(1)

指数函数与对数函数图(2)
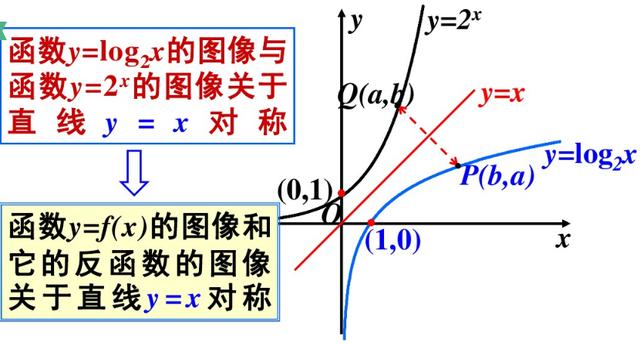
指数函数与对数函数图(3)
例题3、

例题3图
欢迎关注头条号“尚老师数学”!
相关文章
手机黑客需要学什么(新手如何用手机学黑客软件)
本文目录一览: 1、想成为一名的黑客 必须学习哪些课程? 2、当黑客需要学什么 3、黑客们如果入侵了我们的手机,他们会做些什么? 4、黑客要什么学,从那里开始 5、如何变成一个手机黑客...
券包促销实践:一分钟卖了100份
编辑导语:当我们网购时,往往会去寻找一些优惠券,看似一个小细节,实则对促进销售、增加用户的下单量来说是很重要的。本文作者做了一个卖券包的实践,而且将勾当的思考、筹备、设施进程和功效总结分享给各人,但愿...
北京高端夜场招聘 五个方法
.伴随着商务的发展趋势,却出現了假女学妹这类物品,加女学妹也就是摆放在店铺大门口的这些衣着衣服裤子却动也没动的这些人偶,说真话,我对这种假女学妹一点兴趣爱好也没有,更为反感“北京市高端夜总会招聘女学妹...
家装知识科普:石膏线条怎么安装
相信现在有很多的朋友们对于石膏线条怎么安装都想要了解吧,那么今天小编就来给大家针对石膏线条怎么安装进行一个介绍吧,希望小编介绍的内容能够为大家起到帮助哦 石膏线条属于石膏制品的一种,主要是通过与一定比...
wps表格怎么带格式复制
打开文件,进入页面,选定必须拷贝的內容开展拷贝,随后在必须黏贴的部位,右键单击它,挑选选择性粘贴,在弹出来的选择项中挑选必须的文件格式或点击选择性粘贴,弹出对话框,挑选文件格式,点一下明确就可以。 知...
《星球大战7:原力醒悟》720P在线及下载
星球大战7是今年初才在大陆影院上映的,也是此系列第一次出现在中国的影院中。 比起中国影迷,老外对这部影片可以用狂热来形容, 这点可以在IMDB对比豆瓣评分看出来,豆瓣链接 豆瓣评分只有7.2,而...


 免责声明:本站所发布的任何网站,全部来源于互联网,版权争议与本站无关。仅供技术交流,如有侵权或不合适,请联系本人进行删除。不允许做任何非法用途!
免责声明:本站所发布的任何网站,全部来源于互联网,版权争议与本站无关。仅供技术交流,如有侵权或不合适,请联系本人进行删除。不允许做任何非法用途!